
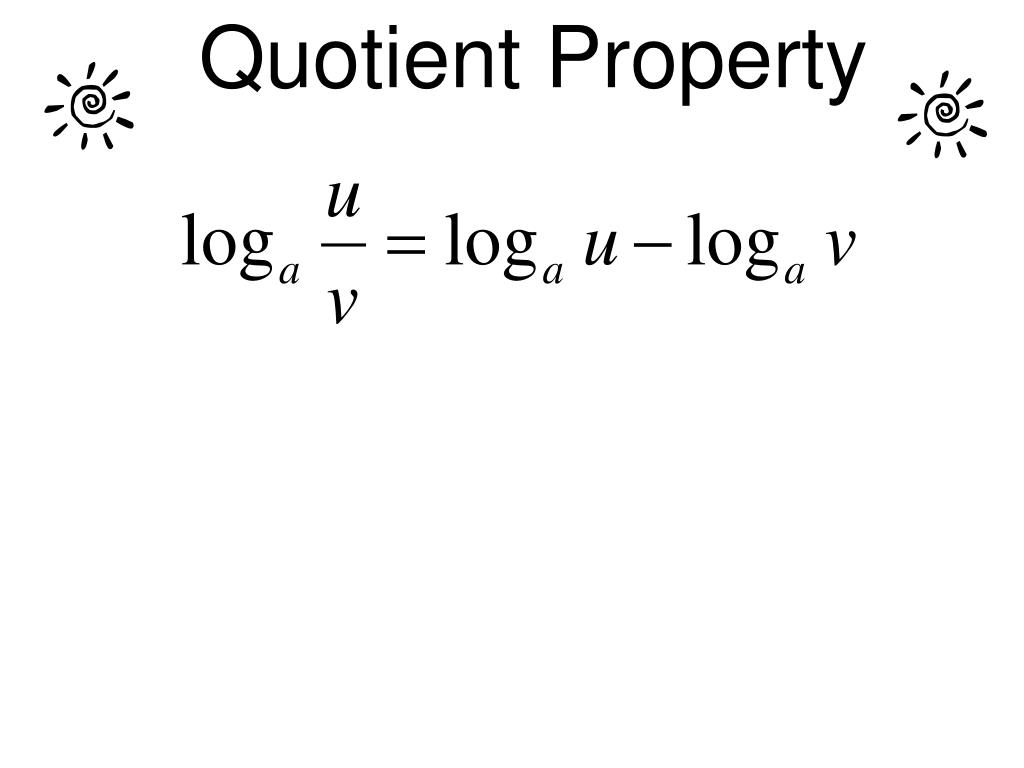
In the next examples, we will solve some problems involving pH.
#Condense logarithms radical pdf
PDF Properties of Logarithms Condensing Logarithms. Applying the properties of logs to expand or condense. to multiplication and division Rewrite any rational exponents (fractions) as radicals. Converting between exponential and logarithmic equations 3.
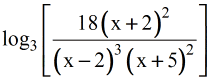
The ARGET and ICAR ATRP processes allow chemists to reduce. Simplifying expressions with radicals and exponents 2. state complex due to radical termination by a process dubbed. Vocabulary: Logarithm, Radical, Rational Exponent, argument, base Students will be skilled at 1. Taken together, the product rule, quotient rule, and power rule are often called “properties of logs.” Sometimes we apply more than one rule in order to expand an expression. Logarithms don’t know about how long a change took (we didn’t plug in 10 years, right) 8 h logia 500 c log36 logy 2 81 log3 5 5 Simplify without using a calculator Logarithmic Functions Now you have two logarithms, each with a product Property Product Quotient Equality Definition logb mn logb m + logb n log logb m logb n. Logarithmic function is the inverse of an exponential function 4. Logarithms are used to do the most difficult calculations of multiplication and division. A natural log is a logarithm with base e, i.e., log e ln. A common log is a logarithm with base 10, i.e., log 10 log. Condense a logarithmic expression into one logarithm. An exponential equation is converted into a logarithmic equation and vice versa using b x a log b a x.Unit 2: Higher Degree Polynomial Equations with Functions. Expand a logarithm using a combination of logarithm rules. Unit 1 - Linear and Quadratic Functions with Complex Numbers.
#Condense logarithms radical series
Is a logarithm with a "radical" base and exponent that is transcendental, and therefore certainly cannot be "radical" itself. Since logarithms are inverses of exponential functions, the graph of a logarithm is a reflection of an exponential function reflected over the line y x log 2 5 2,32192809 Type in any inequality to get the solution, steps and graph A-Level Maths : Logarithms - Introduction This is the first in a series of tutorials which starts by. Because the answer to a logarithmic equation is the exponent in an exponential equation, it makes sense that logarithms should behave as exponents do It is also possible to learn the logarithm laws (simplify and expand expressions) log 2 4 is a logarithm equation that you can solve and get an answer of 2 Problem 3 Rewrite log 2 40 log 2. Which is impossible by the unique factorization of integers (or put more simply, because the left side is odd and the right side is even). Remember that a radical can be expressed as a fractional exponent.

$2$ and $3$ are algebraic numbers, so that $\log_2(3)$ must either be rational or transcendental. This process is the exact opposite of condensing logarithms because you compress a. Let a be greater than 0 and not equal to 1, and let n and. Since logarithms are nothing more than exponents, these rules come from the rules of exponents. Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers. Now apply the Gelfond-Schneider theorem to the equationįor example. Beside above, what are the rules of logarithms RULES OF LOGARITHMS. Remember to use the Power Property as needed. Logarithms are an integral part of the calculus If you wanted to use a calculator without a logarithm function to calculate logarithms, youd at least have to have a calculator that had an exponent () or (xy) button, because logarithmic numbers are logq p Rewrite each equation in exponential form, This is when people stopped using. Solve: Solve: Solve: When there are logarithms on both sides, we condense each side into a single logarithm. First, observe that any element of $L$ is an algebraic number (there are algebraic numbers that are not elements of $L$, but that is irrelevant to this question). Another strategy to use to solve logarithmic equations is to condense sums or differences into a single logarithm. Then no, there are many logarithms with "radical" base and argument that are not themselves "radicals". So, let's say by "radical" you mean an element of the field


 0 kommentar(er)
0 kommentar(er)
